Example
Consider the color.png image. There are five colors but seven regions (two blacks, two greens, one red, one blue and one white).

Open the ImageRegions.java file and review the main method.
BufferedImage image = ImageUtility.getBufferedImage("tiny/color.png");
Color[][] pixels = ImageUtility.getPixels(image);
UnionFind<Integer> regions = new RasterUnionFind(image.getWidth(), image.getHeight());
labelRegions(pixels, regions);
printLabels(regions, image.getWidth(), image.getHeight());
Notice that the labelRegions function goes over every pixel and calls "union" to merge it with its "neighbors" if the pixel has the same color as its neighbors. Before entering the function, we construct a 2D array of pixel colors and a Union-Find data structure. At this stage, the parentID inside the Union-Find must contain each pixel's pixelID. Here is a schematic representation of the parentID array overlayed on a graph representation of the image. (There are no edges between the nodes at this point. We will add edges as we call the union to merge image pixels and form regions.)
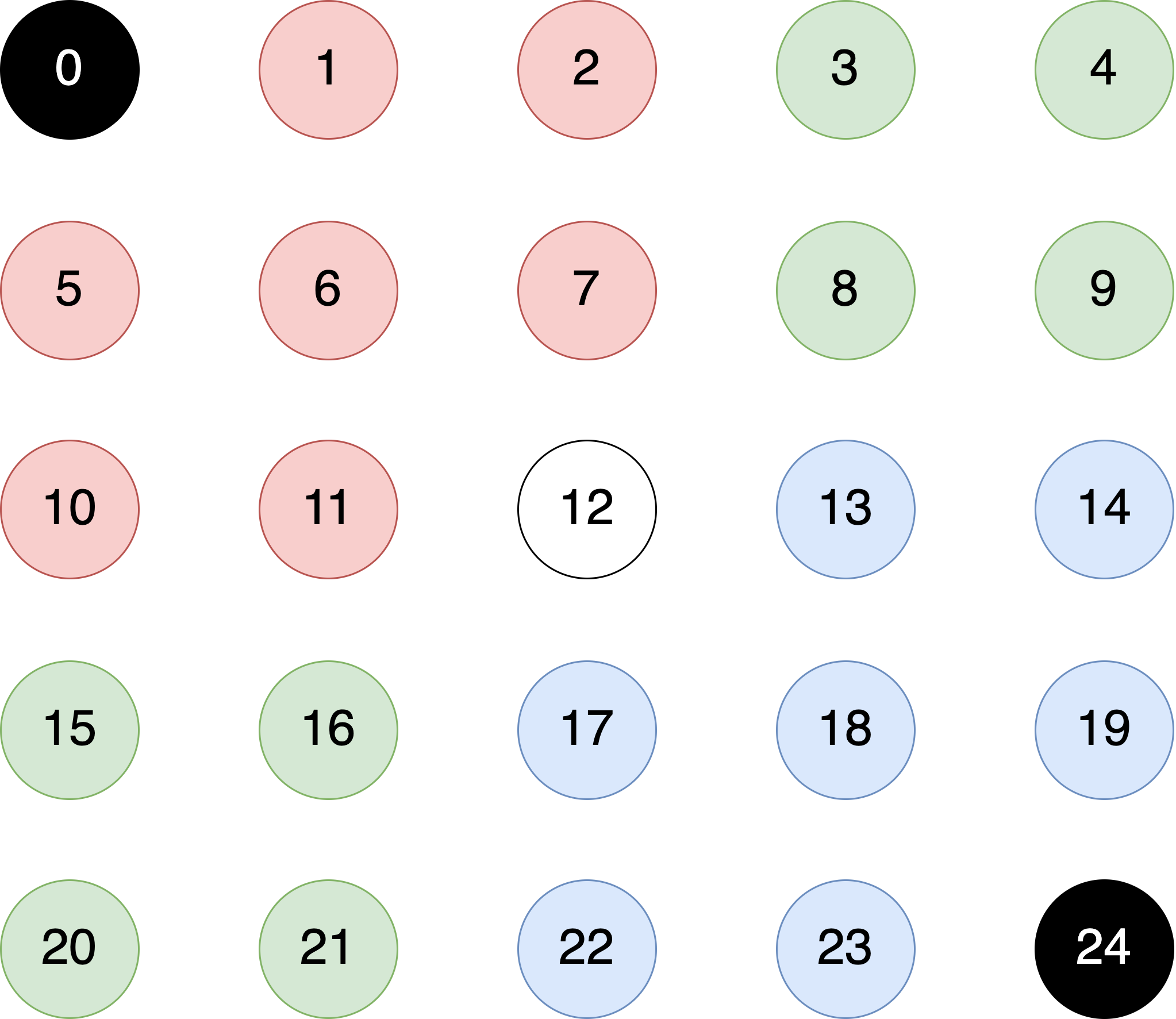
Inside the labelRegions function, we iterate over the elements of pixels array in row-major order.
- The pixel at $(0,0)$ with
pixelID == 0does not have the same color as its neighbors. Therefore, we move on to the next pixel. - The pixel at $(1,0)$ with
pixelID == 1has the same color as its neighbors (to its right and bottom). Therefore, we callunion(1, 2)to merge pixel with ID of $1$ with the pixel with ID of $2$. This must result in the following changes to theparentIDarray.
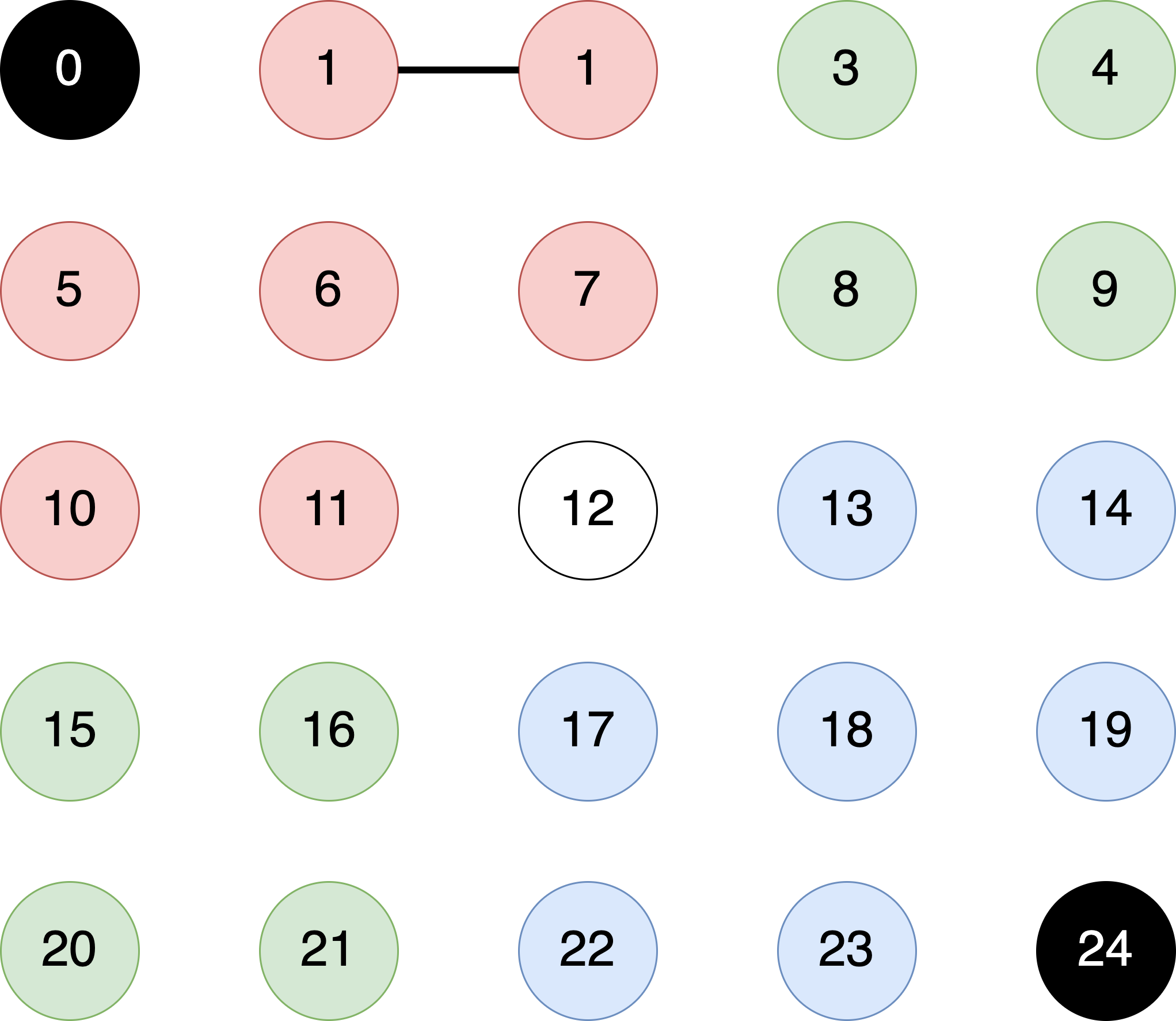
- Next, we call
union(1, 6)to merge pixel with ID of $1$ with the pixel with ID of $6$. This must result in the following changes to theparentIDarray.
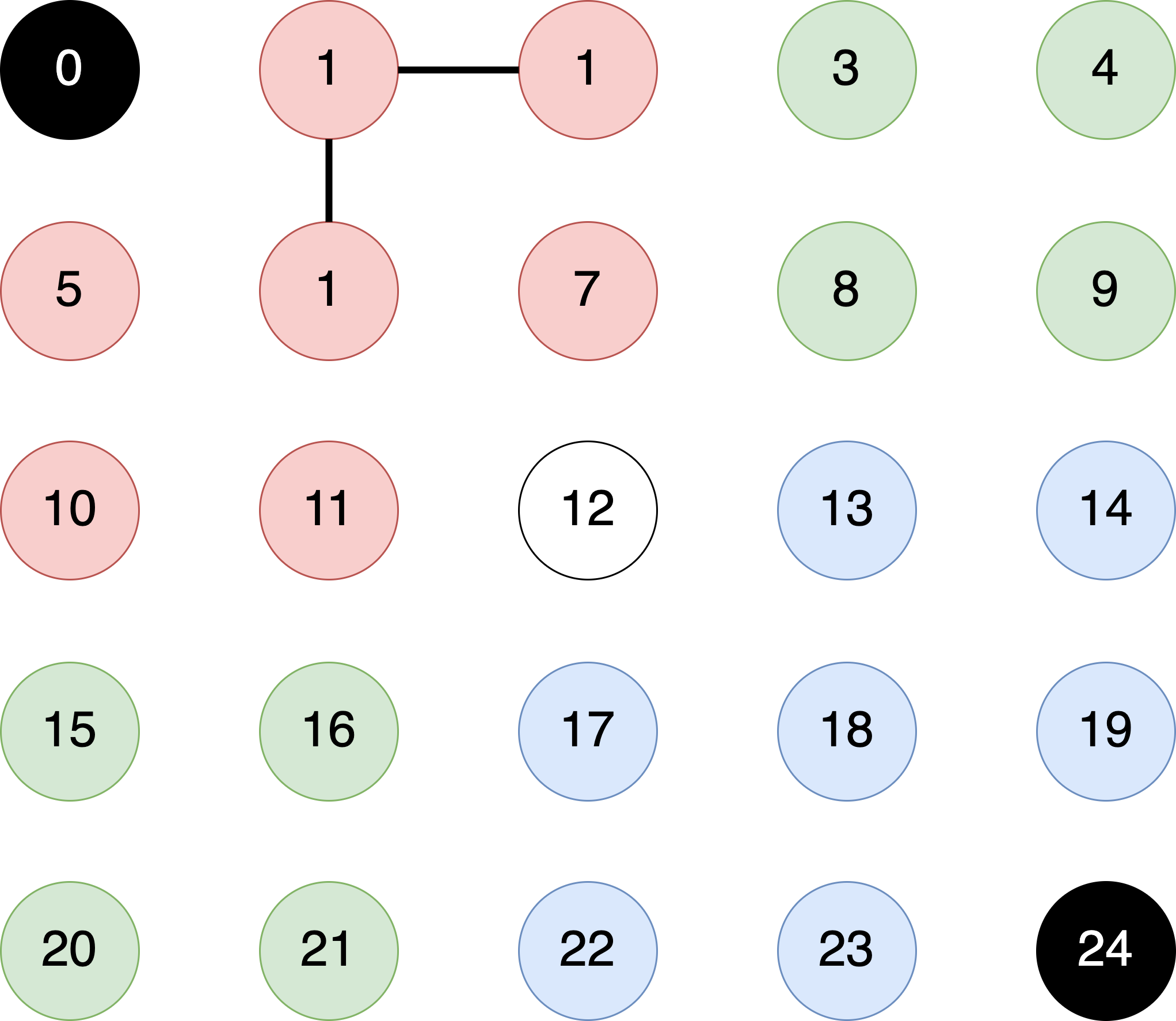
- We now move to the pixel at $(2,0)$ with
pixelID == 2. This pixel has the same color as its neighbor to its left and south. Therefore, we callunion(2, 1)andunion(2, 7). However,union(2, 1)will not result in any changes since these pixels are already connected. Theunion(2, 7)results in the followingparentIDarray.
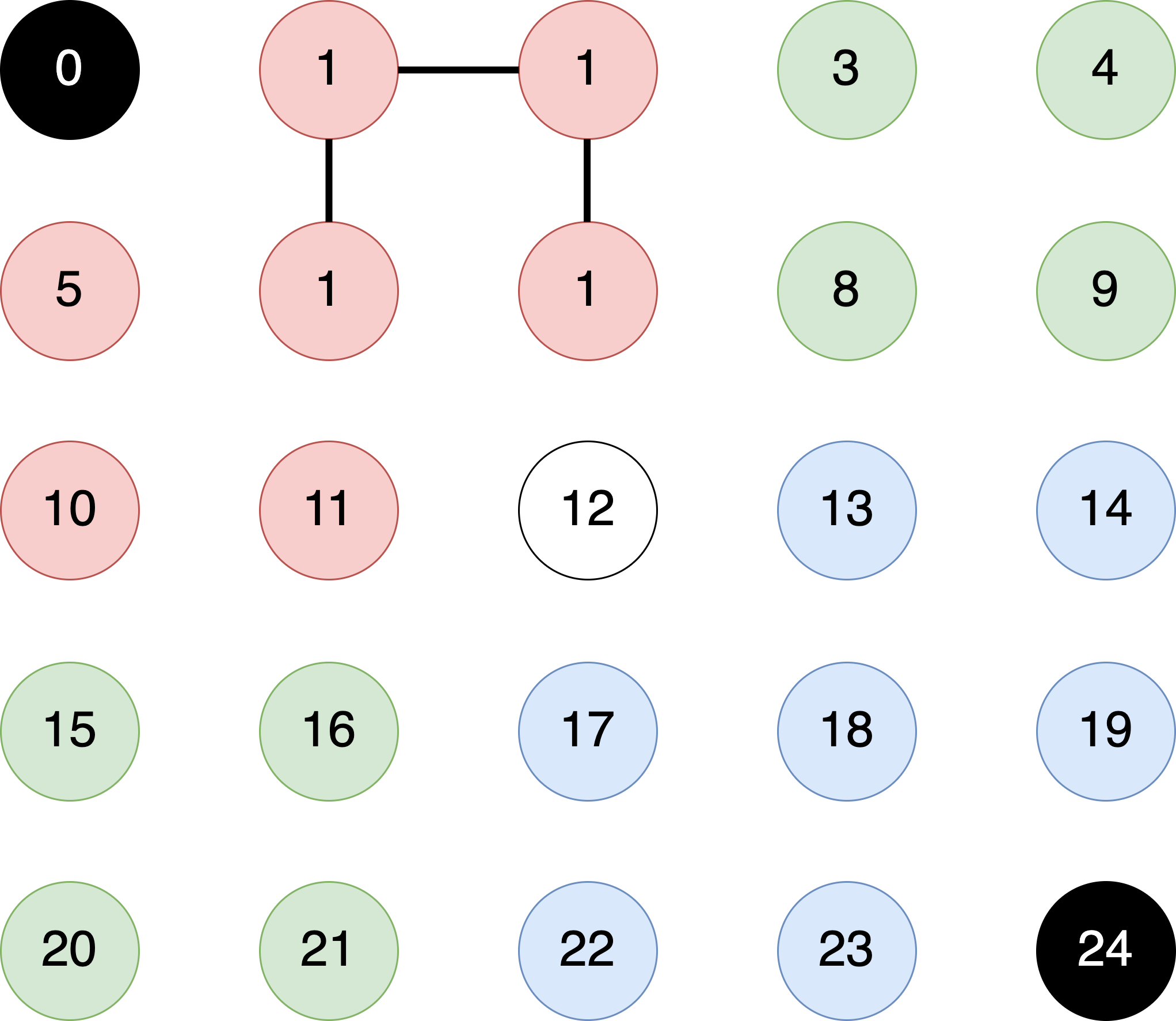
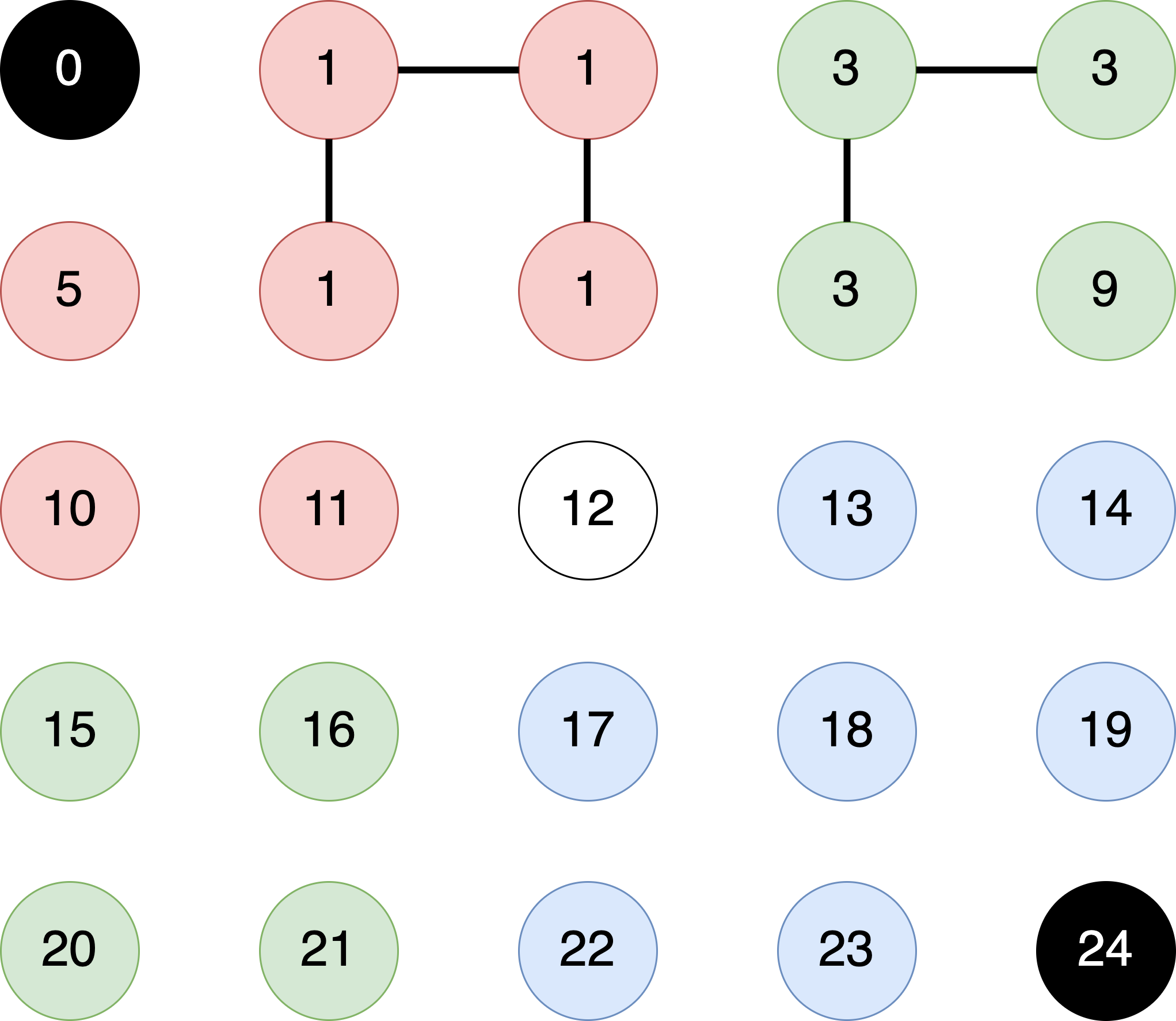
- We now move to the pixel at $(3,0)$ with
pixelID == 3. This pixel has the same color as its neighbor to its right and south. Therefore, we callunion(3, 4)followed byunion(3,8), resulting in the followingparentIDarray.
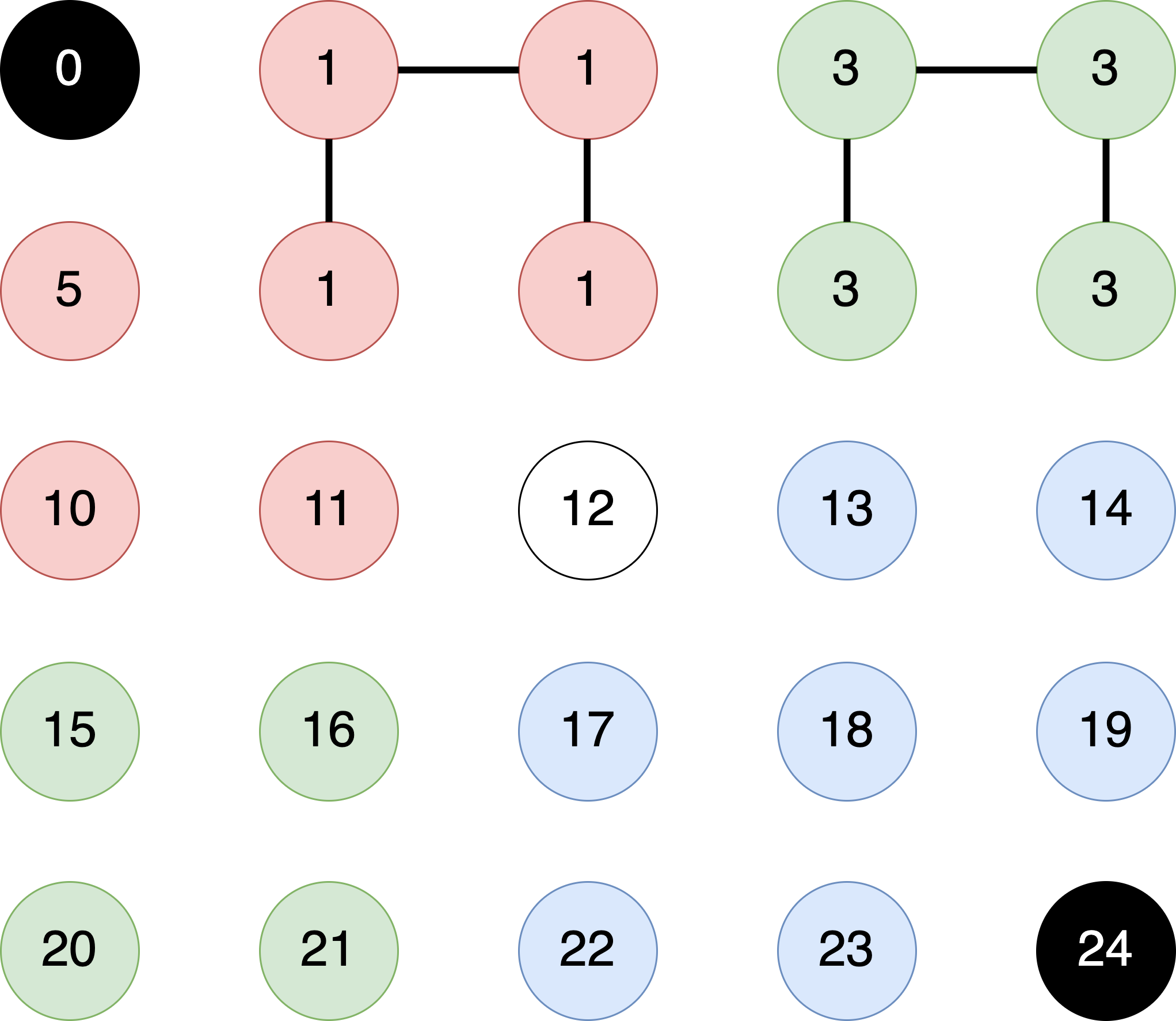
- We then move to the pixel at $(4,0)$ with
pixelID == 4. This pixel has the same color as its neighbor to its left and south. Therefore, we callunion(4, 3)followed byunion(4,9), resulting in the followingparentIDarray.
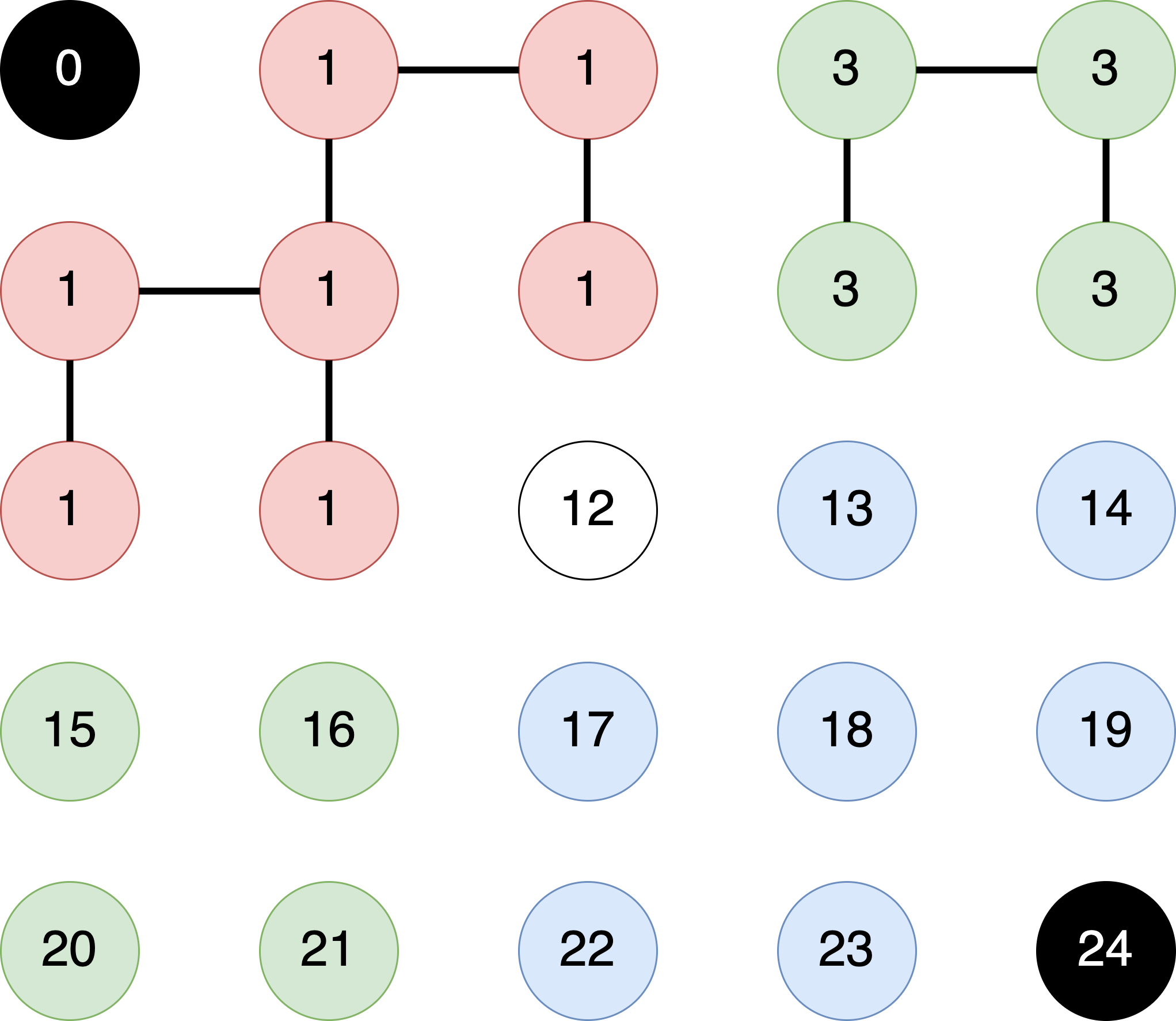
- We are done with the first row. The algorithm will proceed to apply the same process to the second row of
pixelsarray. The application ofunionoperations should result in the followingparentIDarray.
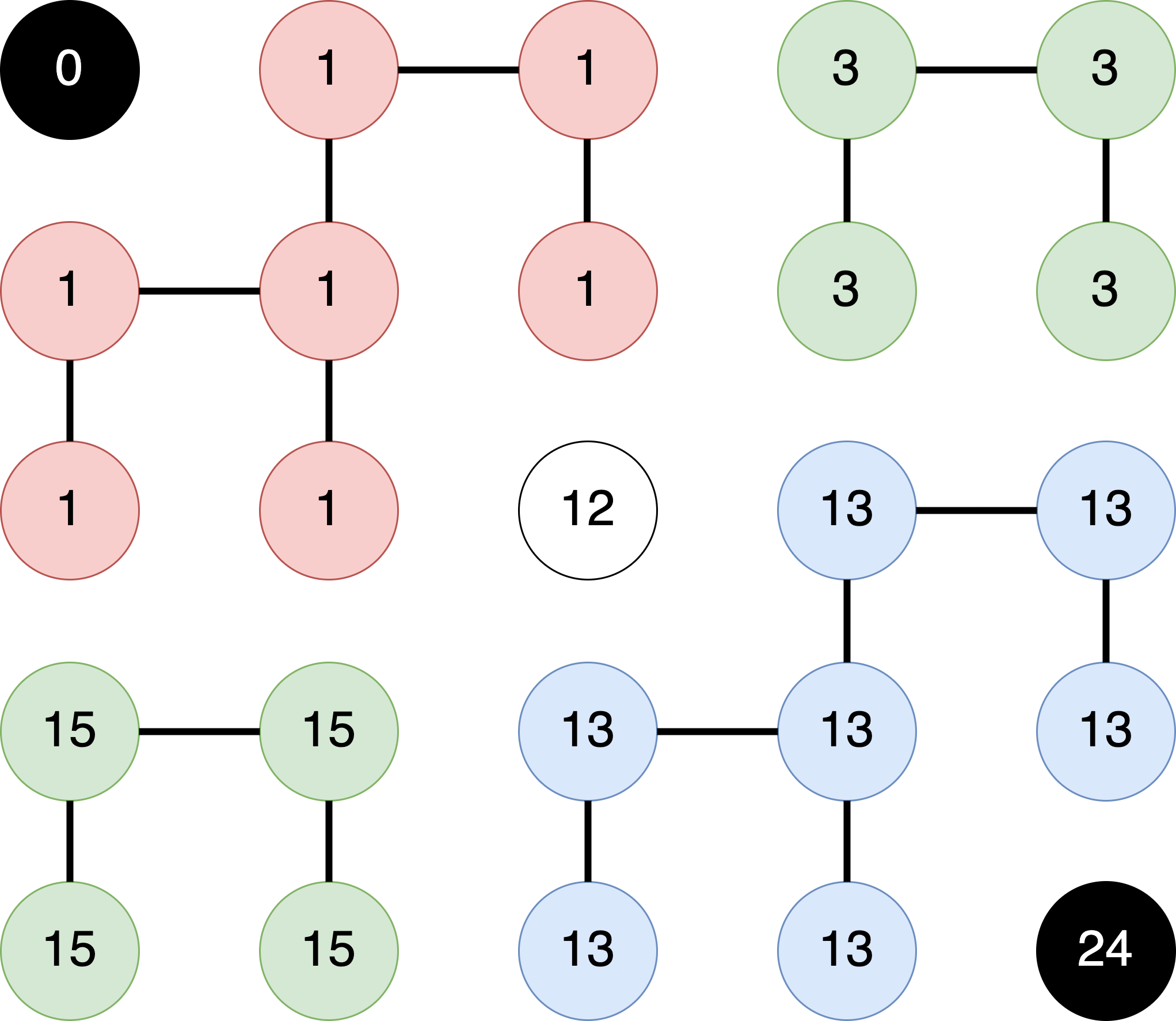
- By the time
labelRegionsis done, you should have the followingparentIDarray.
If you correctly implement the Union-Find data structures and run ImageRegions.main method, you should see the following output:
Number of regions: 7
Region labels:
0 1 1 3 3
1 1 1 3 3
1 1 12 13 13
15 15 13 13 13
15 15 13 13 24
Please skim over the printLabels method and note how it uses the count and find operations of the Union-Find data structure.