Dijkstra's Algorithm

E. W. Dijkstra (1930-2002), the legendary Dutch Computer Scientist (and Turing Award winner), discovered an algorithm for finding the shortest path (in weighted graphs).

Dijkstra's algorithm works by exploring the (unexplored) neighbors of the next vertex with the smallest distance to the source vertex. For this reason, the algorithm is also called Shortest Path First (SPF) algorithm.

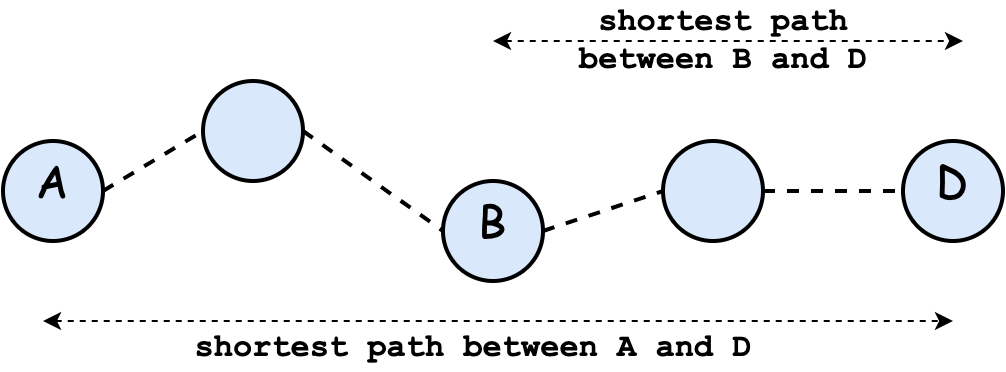
The intuition behind Dijkstra's algorithm is that if vertex $B$ is on the shortest path from $A$ to $D$, then the subpath from $B$ to $D$ is also the shortest path between vertices $B$ and $D$.

For a rigorous analysis and formal proof of correctness, refer to CLRS, Third Edition, Chapter 24, Section 3, Dijkstra's Algorithm on page 658.

Here we will use a demo to understand the steps involved in Dijkstra's Algorithm.

Demo

Exercise Complete the pseudocode for Dijkstra's Algorithm:

for each vertex v
    distance[v] = Infinity
    previous[v] = null
    explored[v] = false
distance[s] = 0   // s is the source
repeat N times
    let v be unexplored vertex with smallest distance
    ________________
    for every u: unexplored neighbor(v)
        d = distance[v] + weight[v,u]  
        if ________________
            _______________
            _______________
Solution 
for each vertex v
    distance[v] = Infinity
    previous[v] = null
    explored[v] = false
distance[s] = 0   // s is the source
repeat N times
    let v be unexplored vertex with smallest distance
    explored[v] = true
    for every u: unexplored neighbor(v)
        d = distance[v] + weight[v,u]  
        if d < distance[u]
            distance[u] = d
            previous[u] = v
Resources