Dynamic Connectivity
Kruskal's algorithm needs a data structure that dynamically (and efficiently) maintains information about the connected components of a graph.
Why does Kruskal's algorithm need such a data structure?
Every edge selected by Kruskal's algorithm must be checked to ensure adding it to the MST would not create a cycle. If the two endpoints of the edge are already "connected" (i.e. there is a path between them), adding the edge will create a cycle.
Such a data structure is called Dynamic Connectivity structure. According to Wikipedia:
In a dynamic connectivity structure, the set $V$ of vertices of the graph is fixed, but the set $E$ of edges can change:
- Edges may only be added to the graph (incremental connectivity);
- Edges may only be deleted from the graph (decremental connectivity);
- Edges can be either added or deleted (fully dynamic connectivity).
After each addition/deletion of an edge, the dynamic connectivity structure should adapt itself to answer questions such as "is there a path between $x$ and $y$? or equivalently: "do vertices $x$ and $y$ belong to the same connected component?".
For example, consider the following graph:
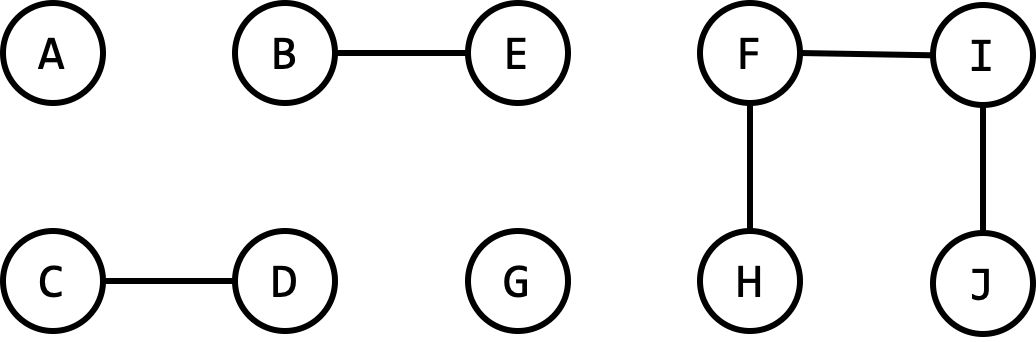
We may ask if there is a path between vertices $A$ and $G$? Or if the vertices $H$ and $J$ belong to the same connected component?
connected(A,G) // false
connected(H,J) // true
Notice "is connected to" is an equivalence relation
- Reflexive: $p$ is connected to $p$.
- Symmetric: if $p$ is connected to $q$, then $q$ is connected to $p$.
- Transitive: if $p$ is connected to $q$ and $q$ is connected to $r$, then $p$ is connected to $r$.
If edges can only be added, then the dynamic connectivity problem can be solved by a Union-Find data structure.
Resources
- Wikipedia Entry on Dynamic Connectivity.