Big-Oh: Mathematical Definition

$$ T(n) \in O(f(n))\Leftrightarrow \exists \; c > 0, n_0 > 0 \; \; s.t. \; \; T(n) \le c\cdot f(n) \; \; \forall \; n \ge n_0 $$

Read it as

$T(n)$ is a member of $O(f(n))$ if and only if there exist positive constants $c$ and $n_0$ such that $T(n)\le c\cdot f(n)$ for all $n\ge n_0$.

Here is a pictorial illustration of the above definition:

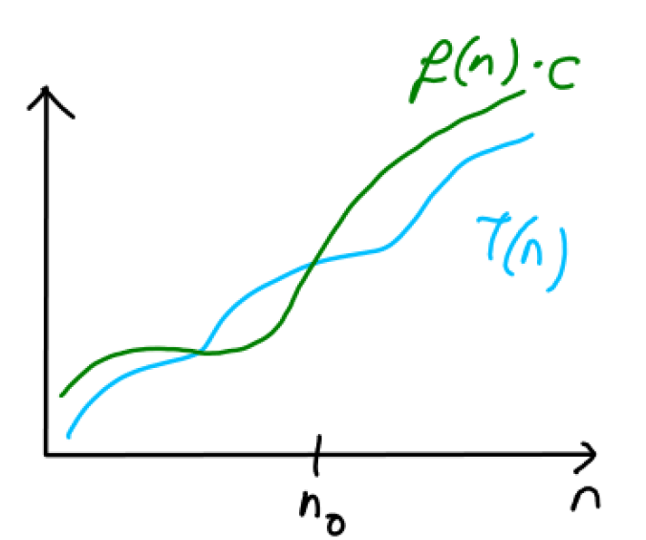
If you want to prove that $T(n) \in O(f(n))$, you need to choose the constants $c$ and $n_0$ so that above definition holds whenever $n \ge n_0$.

Exercise The running time of an algorithm is $T(n)=7n^2+5$. Show that this algorithm has quadratic runtime, i.e. prove $T(n) \in O(n^2)$.

Solution

We can choose $c=12$ and $n_0=1$ for the definition of Big-Oh to hold.

There is not a systematic way to find the constants. However, you can usually play with the $T(n)$ to find one.

$$ T(n) = 7n^2 + 5 \le 7n^2 + 5n^2 \le 12n^2 $$

Resources