Modified Search Problem: Find Distance

Let us further modify the goal of the General Graph Search problem:

Let's make the observation that on a path from $s$ to $v$ and then to $u$ following the edge $(v, u)$, we have $d(u)=d(v)+1$ where $d(x)$ is the distance of vertex $x$ to the source $s$.

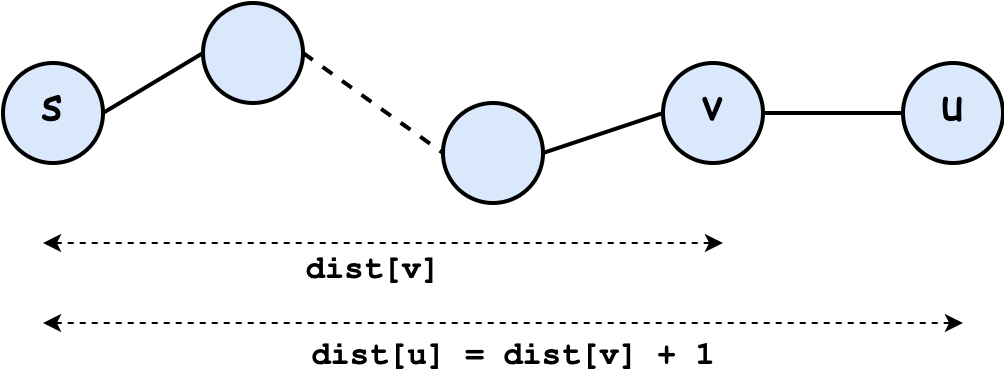
The demo here uses BFS, but we could do the same with DFS!

The following pseudocode describes the BFS algorithm.

// Pre: "s" is the source vertex
explored = {}
explored[s] = true 
queue.enqueue(s)
while (!queue.empty())
    v = queue.dequeue()
    for (w in adjacency[v])
        if (!explored[w])
            explored[w] = true    
            queue.enqueue(w)

Exercise Modify it to include and update the distance collection according to the demo.

distance = {}
explored = {}
distance[s] = 0 
queue.enqueue(s)
while (!queue.empty())
    v = queue.dequeue()
    for (w in adjacency[v])
        if (!explored[w])
            explored[w] = true    
            queue.enqueue(w)
            distance[w] = distance[v] + 1