Adjacent Vertices
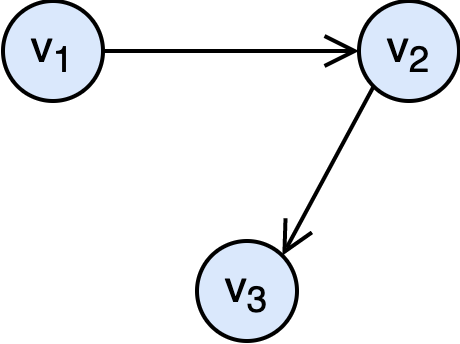
Two vertices that are connected directly with and edge are called adjacent vertices. In the graph below, $v_1$ and $v_2$ are adjacent; $v_2$ and $v_3$ are adjacent; however, $v_1$ and $v_3$ are not adjacent.
Two adjacent vertices forming an edge are said to be incident to that edge. In the graph below, $v_1$ is incident to the edges $e_1$ and $e_3$.
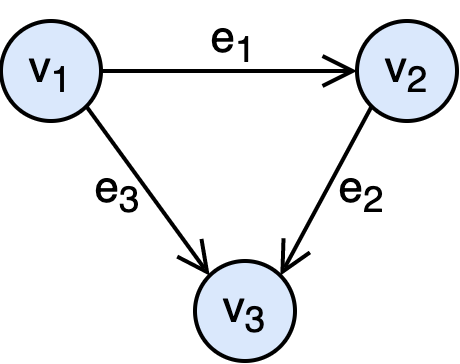
Outgoing edges of a vertex are directed edges that the vertex is the origin.
Incoming edges of a vertex are directed edges that the vertex is the destination.
In the graph above, $\text{out}(v_2)=\{ e_2\}$ and $\text{in}(v_2)=\{e_1 \}$. Note that $v_1$ has no incoming edges and $v_3$ has no outgoing edges.