Lazy Deletion
We learned from the previous exercise that if we delete an item (i.e., set its table entry to null), then when might prematurely stop a search for another one. This could happen for a target item that had collided with the deleted one. We may incorrectly conclude that the target is not in the table (because we will have stopped our search prematurely.)
The issue with removal
Suppose we insert APPLE, BANANA, CAT, and ANT in the table below. Notice ANT must be inserted at index 0. However, it colides with APPLE. Linear probing will take ANT to index 3.
Suppose further we delete CAT in the table below.
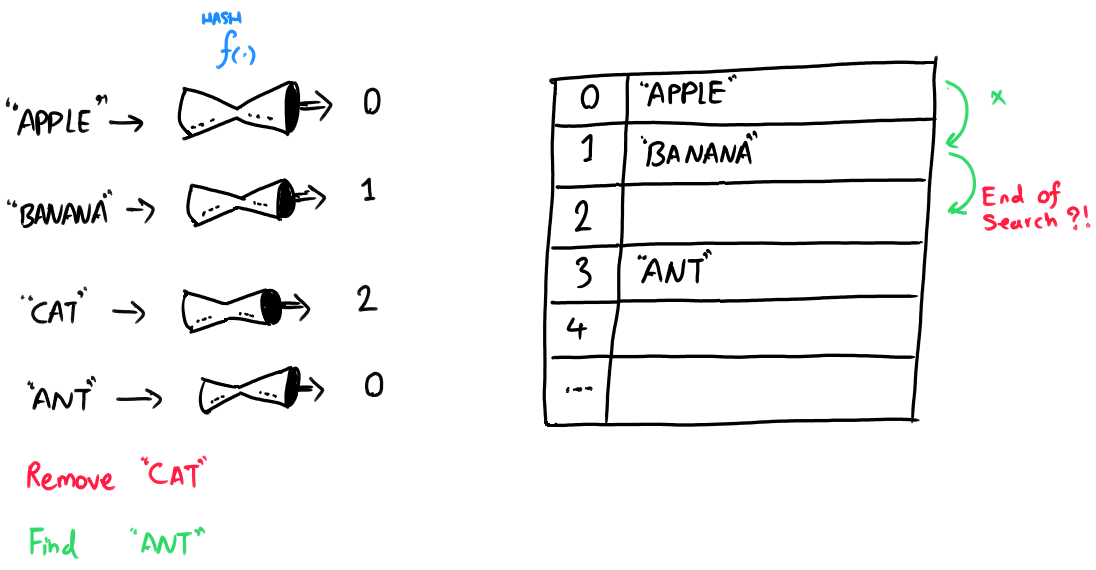
If we search for ANT now, we won't find it! We start the search at index 0 where APPLE is. However, we stop the search at index 2 as it is empty.
The solution is lazy deletion: flag the item as deleted (instead of deleting it). This strategy is also known as placing a tombstone ⚰️ over the deleted item!

Source: craftinginterpreters.com
Place a tombstone!
When an item is deleted, replace the deleted item with a tombstone (to mark it as "deleted").
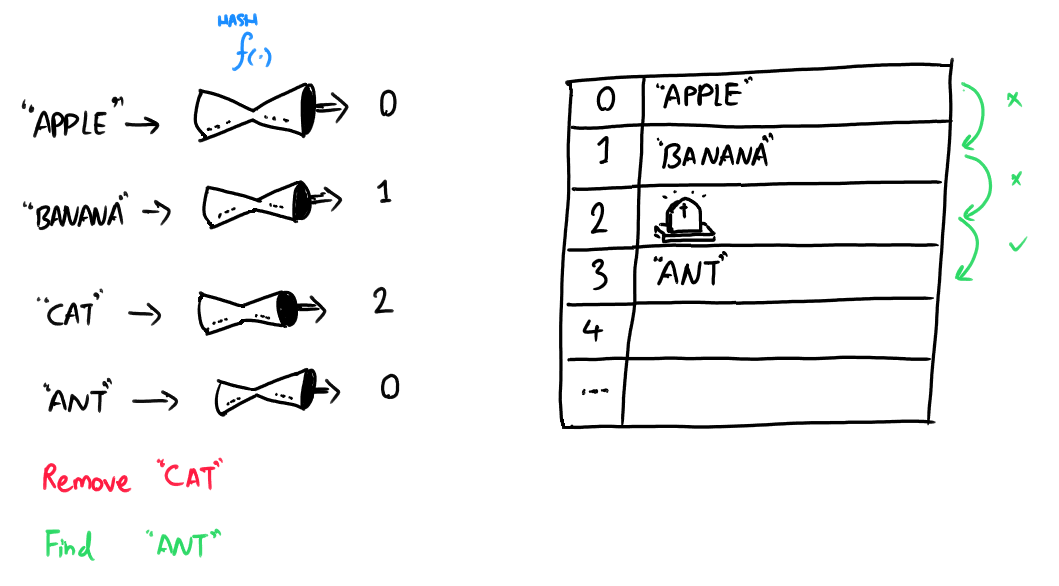
By storing a tombstone (a sentinel value) where an item is deleted, we force the search algorithm to keep looking until either the target is found or a free cell is located.
Future inserts can overwrite tombstones, but lookups treat them as collisions.
For the previous exercise, we insert a tombstone (TS) in place of the deleted entry:
| [ 0 ] | [ 1 ] | [ 2 ] | [ 3 ] | [ 4 ] | [ 5 ] | [ 6 ] | Output | |
|---|---|---|---|---|---|---|---|---|
| Current State | 86 | 700 | 5005 | 1111 | 2332 | 8333 | ||
remove(2332) | 86 | 700 | 5005 | 1111 | TS | 8333 | ||
find(8333) | 86 | 700 | 5005 | 1111 | TS | 8333 | 3,4,5,6: F |
The find(8333) will go over the indices as follows:
[3] --> [4] --> [5] (TOMBSTONE) --> [6] --> FOUND
Without inserting a tombstone in place of $2332$, find(8333) would not know to continue after finding an empty cell at index $5$.