Random BST: Shuffling the Keys

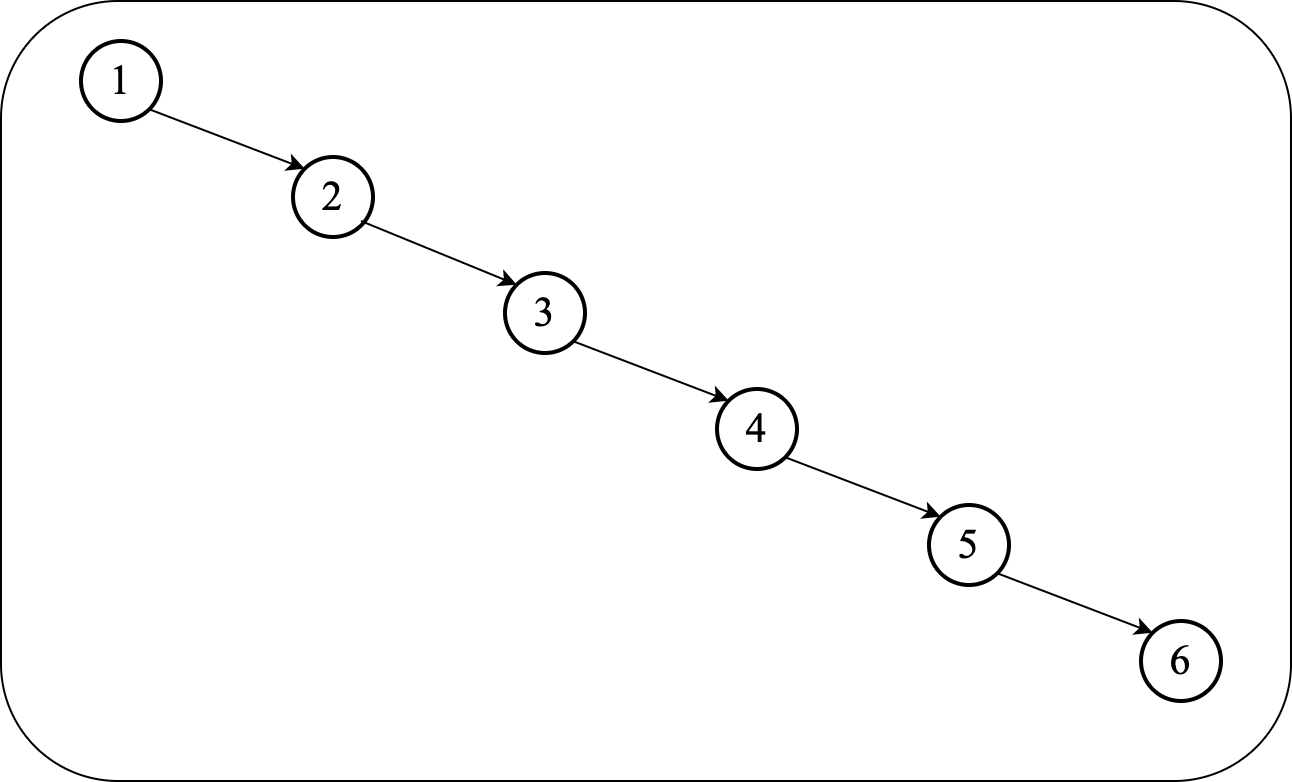
Consider inserting the numbers $1, 2, 3, 4, 5, 6$ into a Binary Search Tree in that order. The resulting BST will have the worst height: $h=O(n)$.

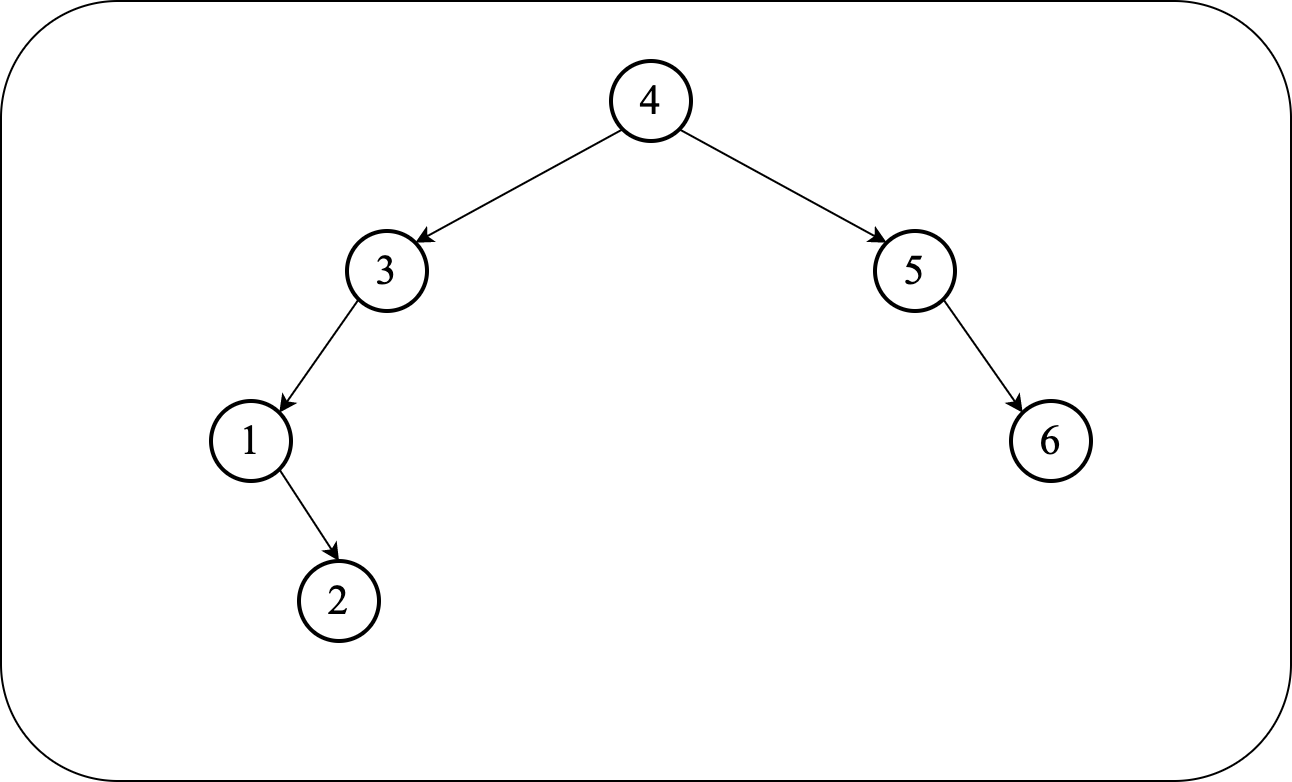
Here is the same input sequence randomly shuffled: $4, 3, 5, 1, 6, 2$. The BST resulting from inserting these values (in order) will have a height closer to the best case: $h\approx O(\lg n)$.

In fact, there are 720 permutations of the sequence $1, 2, 3, 4, 5, 6$. Among these permutations, $32$ will result in $O(n)$ height, $80$ will result in $O(\lg n)$ height and the remaining will be $O(\lg n) < h \ll O(n)$. (Download the starter code and run the Demo.main method.)

Suppose we have, a priori, all the keys that will be inserted in a (regular) BST. We know that if the keys are sorted, our BST will degenerate into a linked list. However, it can be proven (see CLRS, 3rd edition, theorem 12.4) that a simple shuffle of the keys is sufficient to make the BST balanced.

The Treap data structure is designed around this observation. It attempts to create the effects of shuffling the keys as they are inserted (or removed).