Graph Representation: Adjacency Matrix

When it comes to implementing the Graph interface, there are several ways to represent graphs, each with advantages and disadvantages.

The choice of representation will affect the efficiency of various operations of the Graph ADT. Therefore, depending on the problem at hand, you go for one model or another.

Here, we'll see two ways to represent graphs: the adjacency list vs. the adjacency matrix.

An adjacency matrix is a $N \times N$ matrix (array), where element $(i,j)$ is 1 if and only if the edge $(v_i, v_j)$ is in $E$.

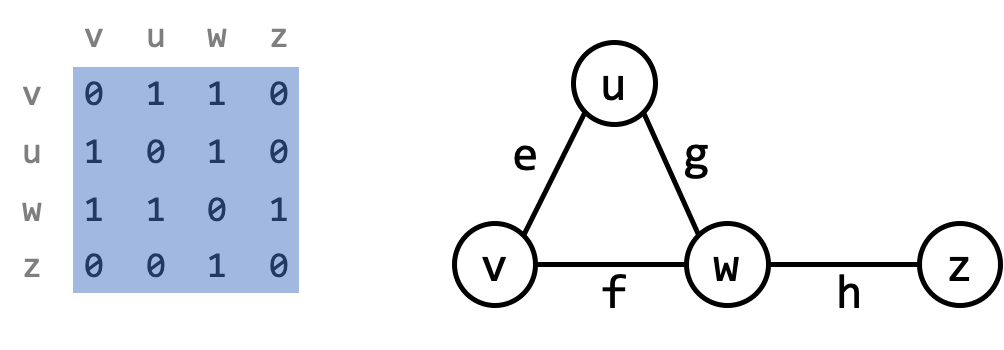
Thus an adjacency matrix takes up $O(N^2)$ storage.

Resources