Perfect Binary Tree
A perfect binary tree is a binary tree in which all interior nodes have two children, and all leaves have the same depth or same level
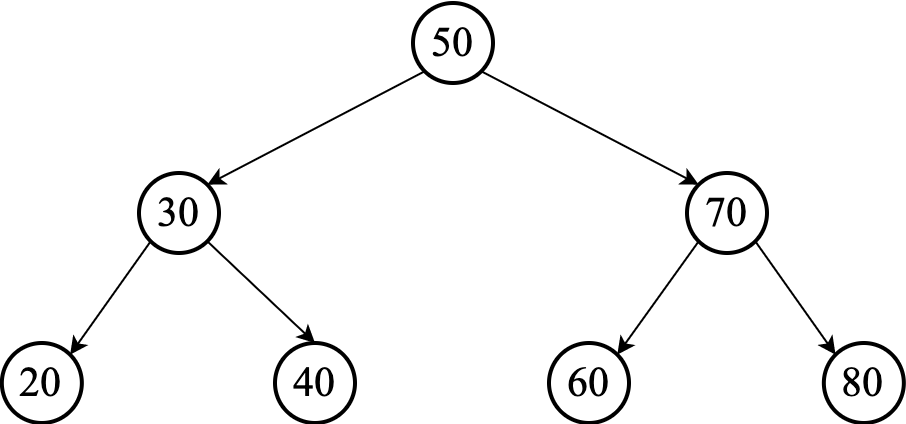
The height of a perfect binary tree is $O(\lg n)$, where $n$ is the number of nodes.
You can verify this by looking at the example above: a perfect binary tree has $1$ node at level (depth) $0$, $2$ nodes at level $1$, $4$ nodes at level $2$, and so on. Thus, it will have $2^d$ nodes at level $d$. Adding these quantities, the total number of nodes $n$ for a full binary tree with depth $d$ is:
$$ n = 2^0 + 2^1 + 2^2 + \dots + 2^d = 2^{d+1} − 1 $$
For example, the full binary tree of depth $2$ above has $2^3 – 1 = 7$ nodes.
Now, considering the formula above for the number of nodes in a full binary search tree:
$$ n = 2^{d+1} − 1 $$
Solving for $d$, we get:
$$ n+1 = 2^{d+1} $$
$$ \lg(n+1) = \lg(2^{d+1}) $$
$$ \lg(n+1) = (d+1)\lg(2) $$
$$ \lg(n+1) = (d+1) $$
$$ d = \lg(n+1) - 1 $$
We know the height of the tree is the depth of the deepest node. So the height of a perfect binary tree is at most $\lg(n+1) - 1$ or $O(\lg n)$.
Resources
- How to Sum Consecutive Powers of 2.
- Wikipedia's entry on Types of Binary Tree.
- Wikipedia's entry on Properties of Binary Trees.